円錐台の表面積は π × ( r1 r2 )× √(( r1 r2 ) × ( r1 r2 ) 高さ × 高さ ) π × ( r1 × r1 r2 × r2 ) で求めることができます。それは,円柱の側面積の半分と考えてよい。つまり長方形の面積の半分と考えればよく, (底辺×高さの半分,底辺はつまり円周のこと) である。 ここでようやく,西元先生の「点対称なグラフの面積は,全体の半分」の意味が読み取れることになる。円柱の体積を求める公式は 半径×半径×円周率×高さ です。 円の面積が 半径×半径×円周率 なので、 円の面積×高さ とも言えます。

公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
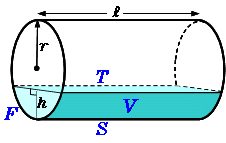
円柱 面積分 ガウス
円柱 面積分 ガウス-面積分 dS z = f (x, y) z x y 領域 上で 関数 の積分を考える.f を微小領域に分解し,そのそれ ぞれの微小領域を底面とし高さ を持つ柱体を考える. f この柱体の(符号も込めた)体積は f dS 微小領域の面積を dS と書けば 面積要素 f dS円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
このときの円柱の高さを、h(=AC)とすると、円柱の体積は、 πb 2 h である。 AB=2a とすれば、切り口は、長径が2a、短径が2b の楕 円を表す。その面積を、S とおく。Y) (2) S 円柱面x2 y2 = R2;円筒 パイプ 体積計算 公式 求め方 チューブ 高さ 長さ 外径 内径 自動 volume
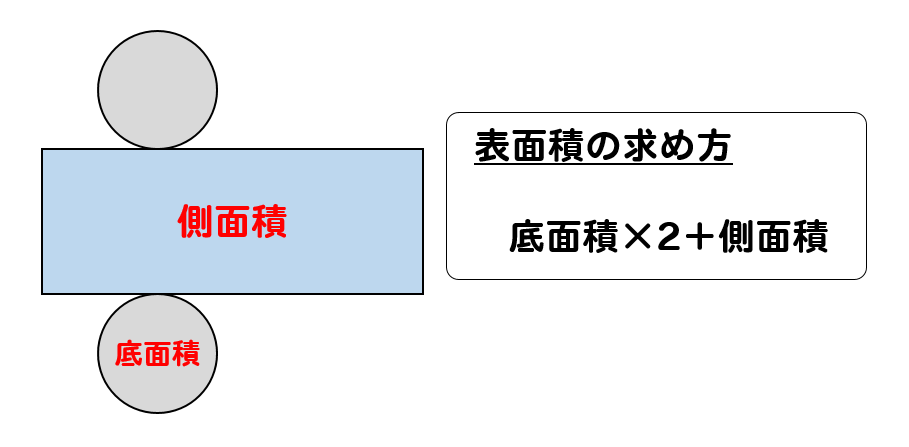
円柱の体積=底面積×高さであることから 円柱の高さ=円柱の体積÷底面積で求めることができます。 答え 8cm 問題④ 棒に長方形の1辺が次のような形でついています。 まずは底面積 (S)を求めます。 「底面積=半径×半径×円周率」で計算できるので「6×6×π=36π (cm2)」が底面積です。 そして、底面積×高さ (h)=円柱の体積ですから、「36π×13=468π (cm3)」が答えです。球の表面積が円の面積の4倍であることの証明 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features
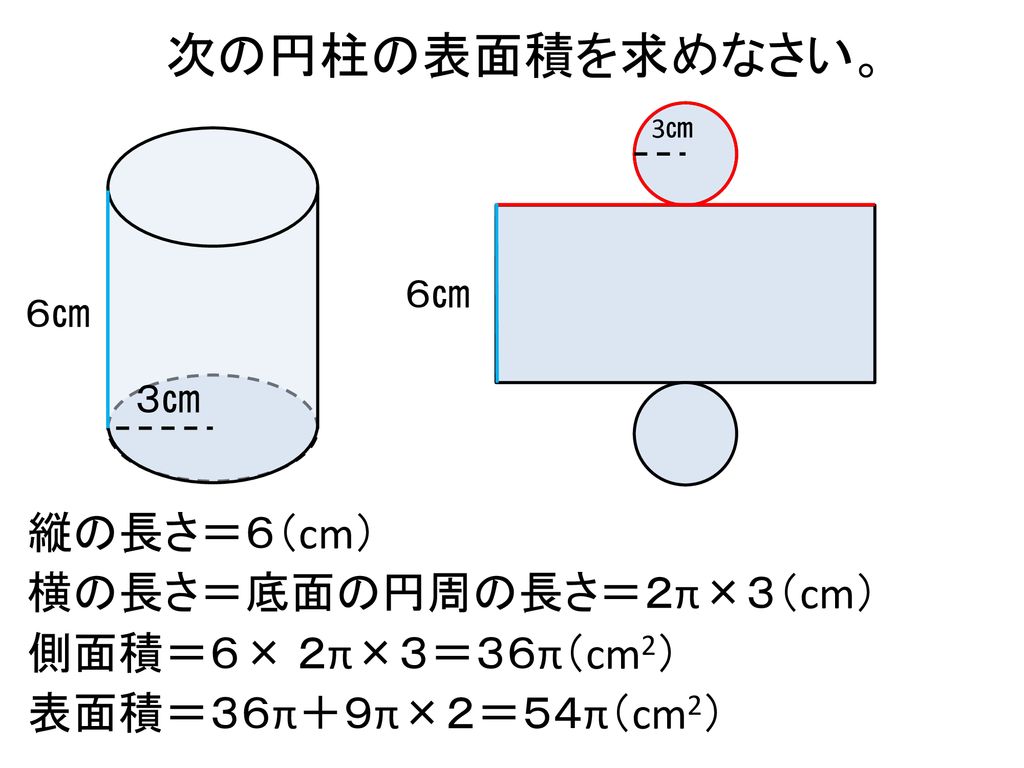
となります。底面の面積\(\pi R^2\)と高さ\(h\)の積です。 円錐の体積の計算 では円錐の体積を計算します。円柱の場合と違うのは変数\(r\)の積分が\(z\)に束縛されている点です。 そこで\(r\)を\(z\)の関数に変換する必要があります。 母線が\(z\)の関数 →面積も小さくなったのではないか? (横から見た図) 半径は短くなったが、接する部分(赤色)が長くなっている. →面積は等しいとイメージできる. どこで切っても面積は変わらない、と考えられる 輪切りの考え方から,球体の表面積=円柱の側面積円柱の表面積を求める公式は、 S = 2πr^2 2πrh = 2πr(rh) で表されます。 このページでは、例題と共に、円柱の表面積の求め方を説明しています。 お使いのブラウザでは JavaScript が無効になってい




円柱の表面積と体積を求める公式 具体例で学ぶ数学




丸棒の重量 円柱の体積と重量の求め方 鉄の場合
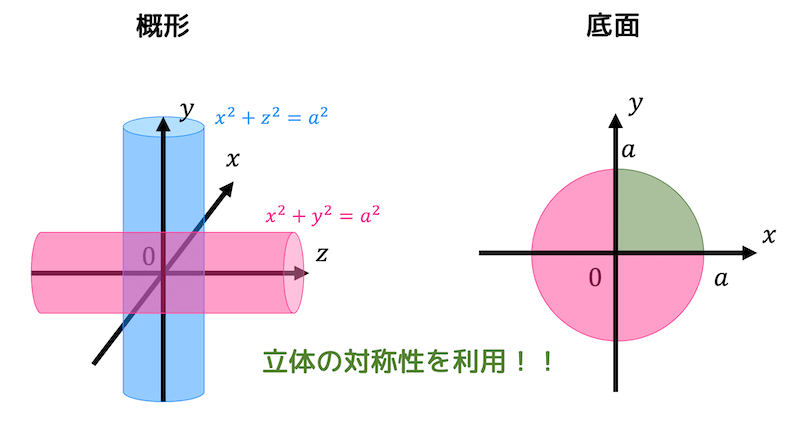
次の法線面積分 ∫∫ S andSを求めよ (1) S 平面x2y 2z = 2が3つの平面x = 0;y = 0;z = 0で切 り取られる部分で原点のある側を負側とする a = (2z;x;問 3 70 (体積の計算) 2 つの円柱 の共通部分 の体積 を求めよ. 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換 というわけで、まずは円柱の体積を求めます。 底面積 円柱の体積 かず先生 体積を求めたら、それをリットルに変換します! 1L(リットル)=1000㎤ つまり、求めた体積 (㎤)を÷1000するとリットルの単位に変換することができます。 ちょっと



円柱とは コトバンク




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
円柱の表面積の公式 底面の円の面積が 、円柱の側面積が のとき、円柱の表面積 は、次の式で求められる。 円柱の面積分についての問題です。 円柱Vの表面積をSとし、その単位法線ベクトルをnとするときの面積分∬(s)a・ndsを求めなさい a = x^2i xyj z^2k V x^2 y^2 = 1, 0 ≦ z ≦ 1 出来れば途中計算も含めて教えていただけたら助かります。A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体




微積5 4 4a 理系のための備忘録




円柱表面積公式 體積 表面積 Gkgnae
0 ≦ z ≦ h, で円柱の側面の正の単 位法線ベクトルは内部から外部に向かってひくものとする球の表面積=円柱の側面積(アルキメデスの発見) 球の体積と表面積の関係から 球の表面積や体積を求める公式は,特に生徒が暗記に頼ってしまいがちな箇所ですが,暗記の覚え込みだけで得 た知識は,定着が悪く,応用も効きにくくなります。練習問題で理解を深める! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかが




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



角柱と円柱の体積 算数用語集
2.円柱の体積を求める方法 円柱 とは、下の図形のように上下の底面が円の形になっている立体図形のことです。 円柱の体積を求めるには、 円柱の体積=底面積×高さ を計算すれば導くことができます。 したがって、底面積は円の面積を使えばいい練習131 球面x 2 y 2 z2 = a の表面積を求めよ。( z = p a ¡x2 ¡y2 の fx2 y2 • a2g 上の曲面積の2倍) 宿題131 1) 二つの円柱x2 y2 • a2, y2 z2 • a2 の共通部分の体積を求 めよ。(変数変換は必要ない) 2) 円柱面x2 y2 = a2, 平面z = 0, 曲面z = x2 y2 で囲まれた領域の体積 を解 円柱x 2y 5 Rxはz 方向に無関係であるから,球面x2 y2 z2 = R2 がこの円柱によっ て切り取られる部分S はxy平面に関して対称.したがって,S のz = 0の部分S の曲面積を



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ



1 この球の体積と円柱の体積の比を求めなさい 2 この球の表面積と円柱の Yahoo 知恵袋
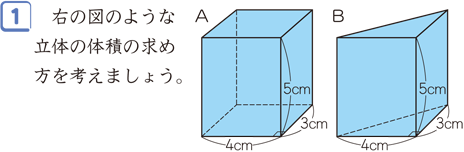
角柱や円柱の体積を,公式を用いて求めることができる。 (数量や図形についての技能) 角柱や円柱の体積は,底面積×高さにまとめられることを理解する。 (数量や図形についての知識・理解) (2)単元の評価規準 ア 算数への 関心・意欲・態度円柱の体積 $v$ は、 円周率× 半径 × 半径 × 高さ 円柱の表面積 $s$ は $2$×円周率× 半径 × 半径 +$2$×円周率× 半径 × 高さ




円柱の表面積の求め方 公式と計算例




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




中学数学 円柱の体積の求め方と公式 塔をモチーフ なぜか分かる はかせちゃんの怪しい研究室



相似と体積比 2 ネット塾




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




角柱 円柱の表面積と体積の公式 数学fun




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



円柱の表面積は 1分でわかる公式 求め方 計算 側面積 底面積との関係




円柱の表面積と体積を求める公式 具体例で学ぶ数学




至急 円柱の切断の側面積 急ぎで教えて欲しいです 円柱の切 数学 教えて Goo



U9j580gf8iba369ji2w Xyz P 296




中1 数学 6 2 角柱 円柱の表面積 Youtube




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube




円の面積 円柱の体積と比重 日々自己の鍛練



円柱の求め方について なんですが 小学校でやったはずの円柱の体 Yahoo 知恵袋




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典
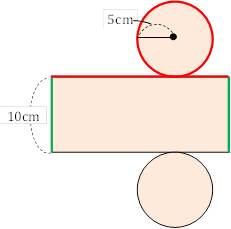



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




円柱の表面積の求め方 公式と計算例
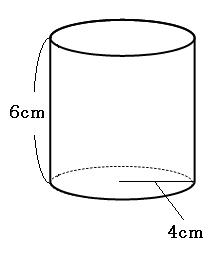



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




なぜこの円柱の問題の時 側面積の時2pをかけるのですか Clear




4 Descubre Como Resolverlo En Qanda




円柱の表面積の求め方 側面積の考え方をマスターしよう 中学数学 理科の学習まとめサイト



Q Tbn And9gcqjobggcmt23 2z3kno11yv3jyxklvrxkobpwlhwovwikso5zii Usqp Cau



1




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




中2数学 p 11 どちらの側面積が大きいの Youtube




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




円柱の表面積の求め方の基本 現役塾講師のわかりやすい中学数学の解き方
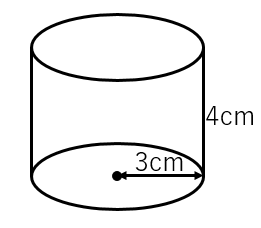



円柱の表面積と体積を求める公式 具体例で学ぶ数学
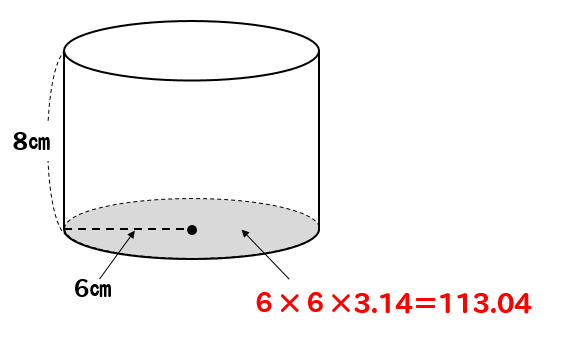



算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




球の表面積と体積の公式 数学fun




角柱や円柱の表面積の求め方を教えてください Clear
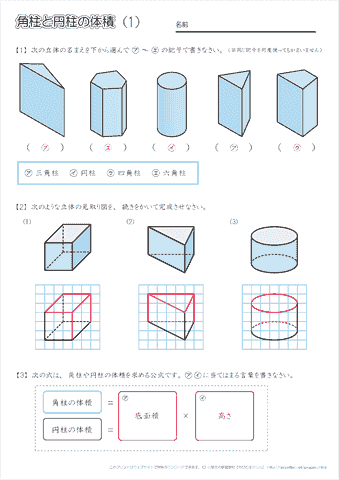



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




円柱の水槽に球を入れる問題 苦手な数学を簡単に




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Math 円柱 内接する球 円錐の体積と表面積 働きアリ




相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア




円柱の表面積 Youtube




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円柱の体積の求め方 公式 小学生 中学生の勉強



5 8 円柱を3等分した図形の体積と面積を求めるには さんすうがく
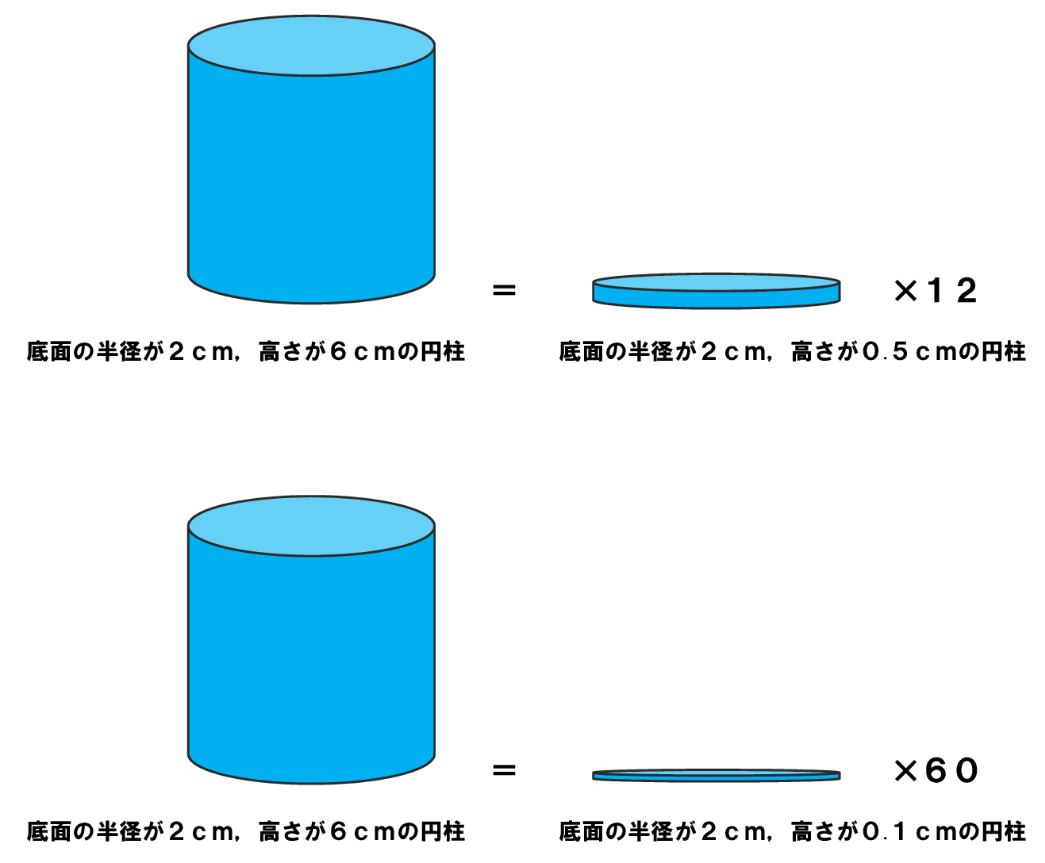



もたこ博士の算数工房 算数から数学まで




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円柱の体積の求め方 公式と計算例




Open Sesame Descubre Como Resolverlo En Qanda
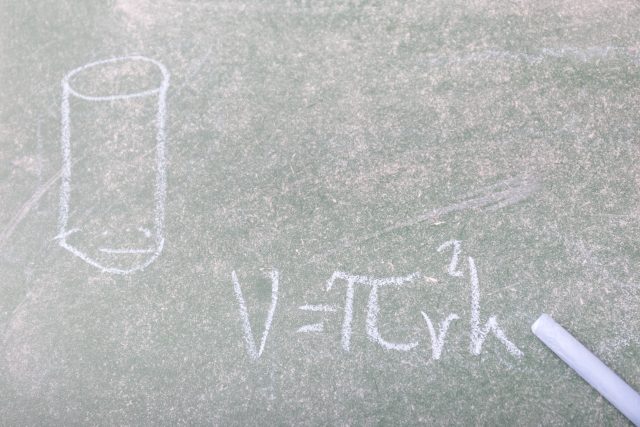



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



1




初等幾何 球の表面積を求める 大人が学び直す数学




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




円柱p Qの体積と面積と比を教えてください 中二の文字式の利用です Clear
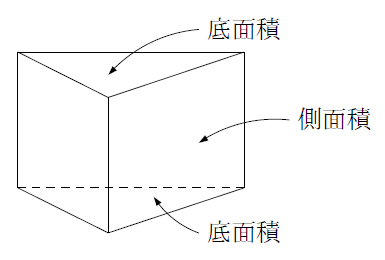



角柱 円柱の表面積 まなびの学園




110 Bar6gm Descubre Como Resolverlo En Qanda




円柱の体積 表面積 側面積 計算機 かんたん計算機
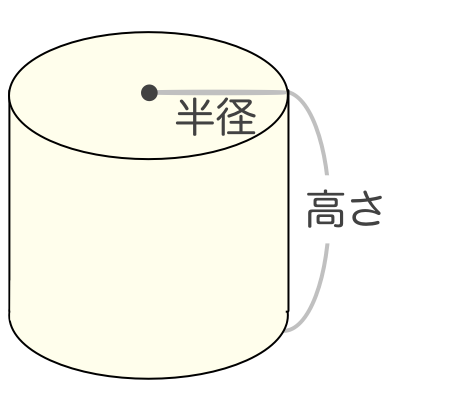



円柱の表面積 簡単に計算できる電卓サイト




2 を途中式を含めて教えてください Clear




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト



Www City Hadano Kanagawa Jp Www Contents Simple Kuukan410 Pdf
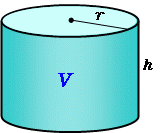



直円柱の体積 高精度計算サイト




円柱の表面積 Youtube



一部が欠けた直円柱の体積 高精度計算サイト



1



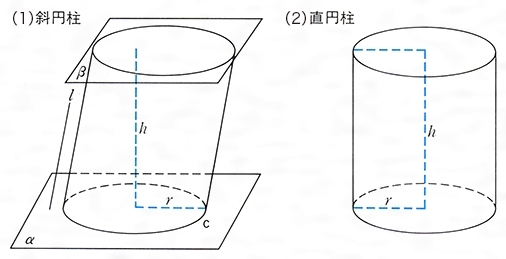
斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
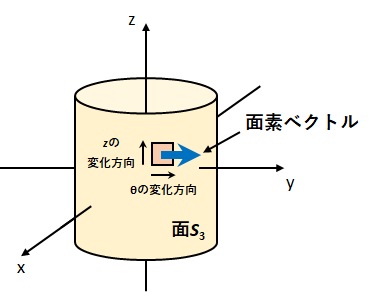



ベクトル解析 面積分 概要と例題 平面 球面 円筒面上での面積分




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




円柱の表面積 チーム エン



円柱とそれに内接する球の表面積比と体積比について 久保塾 今治市の学習塾




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



断面積の意味は 四角 長方形 や円筒 配管 や円柱の断面積の計算方法 求め方 は 単位はmm2 水平断面と鉛直断面 垂直断面 ウルトラフリーダム




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




تويتر はりねずみ 中学校数学科 على تويتر ちなみにこれがなんで成り立つのか最後までよくわからなかった 結果的にそうなるだけなの カバリエリの原理みたいに普遍的な原理があるの 一方で球の表面積 が円柱の表面積の2 3倍ってのもなかなかきれいなんだけど 体積




円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円柱の体積の求め方 公式 小学生 中学生の勉強



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download
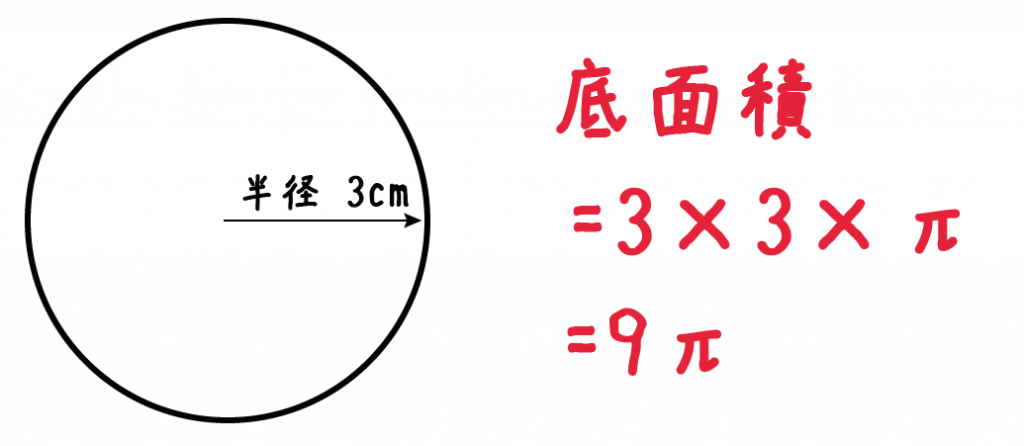



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係
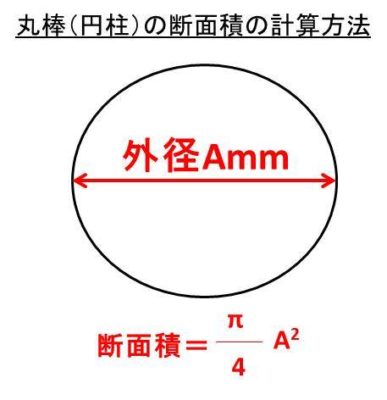



鉄やステンレスの円柱の重量計算 丸棒の重さ 質量 の求め方 白丸くん




中学1年生 数学 無料問題集 角柱や円柱の体積 おかわりドリル
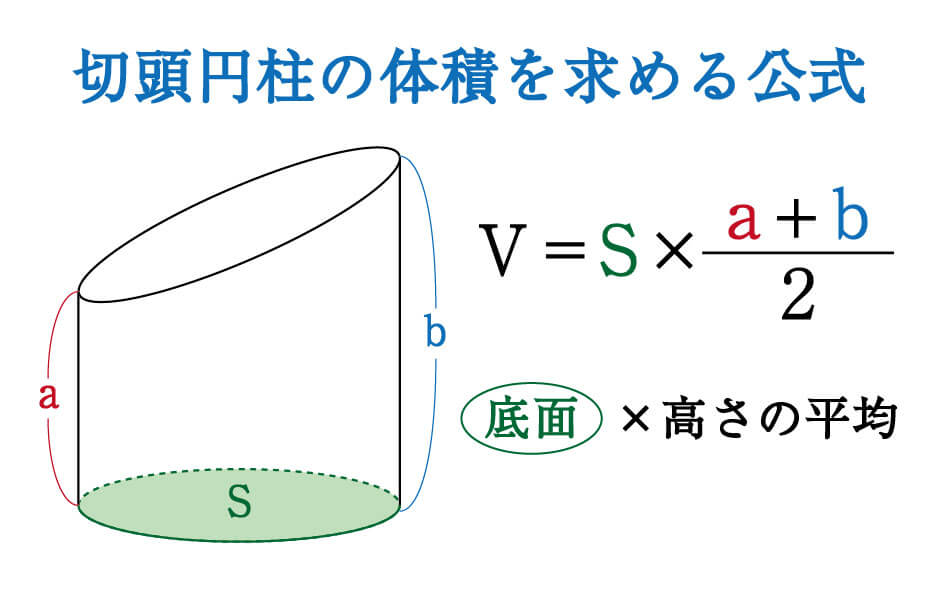



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
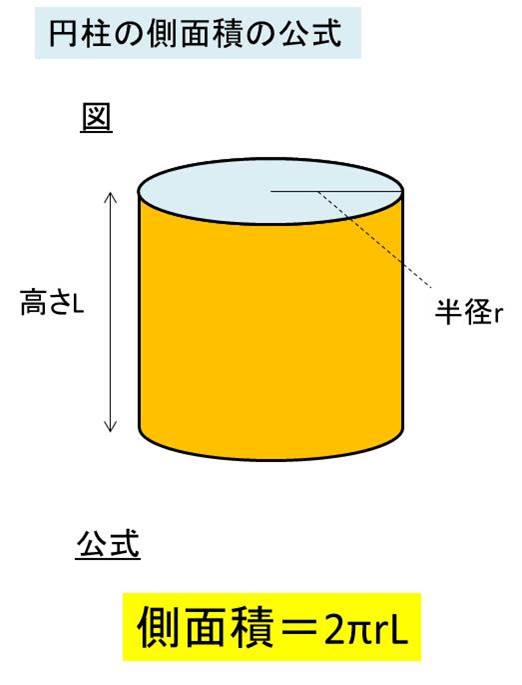



円柱の側面積 底面積 表面積を求める方法 白丸くん



0 件のコメント:
コメントを投稿