例えば7人の学生a~gのうちから3人選んで一列に並べる並べ方は であることは先ほど順列の単元で見ましたが、その中で abc,acb,bac,bca,cab,cba の6つは同じ(a,b,c)からなるため組み合わせでは同一のものと考えます。Abc、acbと2通りの並べ方があることがわかりますね。 よって、(1)の答えは2通りとなります。 次に、全体を考えていきます。 aを先頭にして並べる方法が2通りでした。 ということは同じように考えて bを先頭にした場合も2通り組み合わせ方の図や表をかい・他の場合の組み合わせの 前時の組み合わせ方を適 5 て,落ちや重なりなく考えるこ 問題を解く。 用した表現によって,説明 とができる。 をかく。

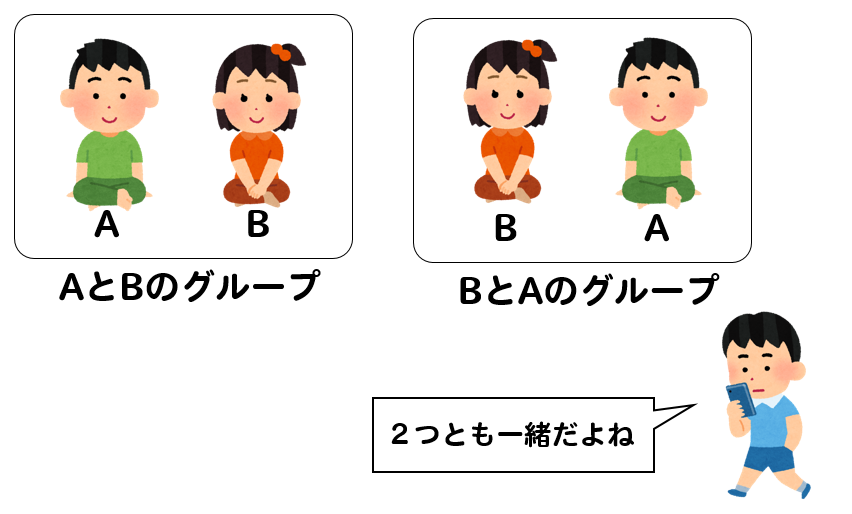
この問題を2枚目の写真の解答1の方法で解きたいのですが 答えが合いません Clear
並べ方と組み合わせ方 答え
並べ方と組み合わせ方 答え-組み合わせの計算 1 ステップ1 並べ方と選び方の区別 1 A、B、Cの3人の小学生がいます。 ⑴ 3人の中から2人を選んで並べます。 ① 並べ方を、樹形図を使ってすべて書きなさい。 ② 並べ方は全部で何通算数「ならべ方と組み合わせ方③」 教p15 4 ックの結果(入ったか、入らなかったか)にはどのような場合がありますか。 ①入った場合を〇、入らなかった場合を×として、 1回目が入った場合を図や表を使って調べましょう。




並べ方と組み合わせ方 その2 家庭学習レシピ
4 先ほど, 「5 つの文字から異なる3 つの文字を並べる並べ方」を調べ, それが60 通りであるこ とをみました。今度は, 並べる必要はなく, 選び出す選び方です。今回は文字ではなく, 5 種類のリ ボンですが。これは, 次のように考えることができます。 並べ方の60 通りの中に, (赤;青;黄) の3 種の 順列(並べ方)とはまた違った数え方をしないといけない組み合わせ。 うまく数えるコツをつかめるととても楽に問題を解くことが出来る単元になります。 今回の記事では、組み合わせの数の数え方について書いてみたいと思います。 小 「うさぎの記念撮影」をするために、まろん、きなこ、るか、そら、ももやまの5匹の並べ方を考えたい。 (1) 並べ方は全部で何通りですか。 (2) 右端が「るか」となる並べ方は全部で何通りですか。 (3) 「まろん」と「きなこ」が隣同士となる並べ方は全部で
男子の両端とその間の5か所のうち1か所にAとBを並べていれる。 そのときAB,BAの2つの並び方があるので \(5\times{2}=10\)通り 最後にBの隣を除く5か所のうちの1か所にCをいれる。 したがって、 \(24\times{10}\times{5}=10\) 答え 10通り おわりにべ方と組み合わせ方 並べ方③ 遊園地にパレードがやって来ました。 赤、白、青、黄の4本のはたを持っています。4本のはたの 並び方は、全部で何通りあるでしょうか。 赤が1番前だと 6通り (6パターン) 白が1番前だと 赤 赤 6通り11 並べ方と組み合わせ方② 学 年 組 氏 名 1 さとしくん,たかしくん,まさしくん,やすしくんの4人が,リレーで走る順序を決 めています。 (1)さとしくんをA,たかしくんをB,まさしくんをC,やすしくんをDとします。1
1 順列と組み合わせの違い 「5人の中から2人並べる。」 「5人の中から2人選ぶ。」 この2つの違いは分かりますか?分かる方は「 2順列 公式 」に進んでしまって構いません。 順列と組み合わせを考えるとき、ごっちゃになってしまう人がいます。(2) 班長と副班長の決め方は全部で何通りですか。 答え (1) (2) 2 1,2,3,4の数字が書かれたカードが1枚ずつあります。 (1) 4枚のカードのうち2枚を並べて2ケタの整数をつくると、何通りつくれますか。 式 答え並べ方と組み合わせ方のちがい 校外学習のコースを決めます。3か所の候補から2つ選びます。 ・都庁 ・浅草寺 ・スカイツリー ①どんなコースがありますか。 ②どんな組み合わせがありますか。



算数 場合の数の解き方は 問題別に考え方を解説 数スタ



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校
つまり,5個の を2本の仕切り棒で区切って左から順にa, b, cに置き換えることになる。 と|の並べ方が変わると,a, b, cの組合せも変わる。もっとちゃんと言うと, と|の1つの並べ方と,a, b, cの組合せが1対1対応する。 よって,求める組み合わせの総数は これを 『 組み合わせ 』 といいます。 順列 は、 違う選び方、別のもの、つまりは重複したものではない と考えています。 つまり、 あるn個のものからr個選んで、 ・「順序よく1列に並べて。並び方が逆でも重複したもの(無視)としないで並べてね。 この2種類の問題では、それぞれ答えが変わってきます。 ①は順列で、答えは 5 p 2 =5×4=通り ②は組み合わせで、答えは 5 c 2 =5×4÷2=10通りになります。 今回は、そんな順列と組み合わせの数の考え方についてです。




アルバルク東京 小学6年生向け算数ドリル 渋谷区など都内公立小学校に配布 シブヤ経済新聞



トップ 100 並べ方 と 組み合わせ 方 問題
順列と組み合わせの概要・公式・違い 順列と組み合わせの計算方法は記事の後半に回して、まずは 順列と組み合わせとは何なのか、その2つの違い も含めて紹介します。 順列とは、いくつかのものを順序をつけて列に並べる 並べ方 の総数です。 組み合わせとは、いくつかの要素の集ま 一応授業ノートです 小6 算数 並べ方 組み合わせ方 並べ方と組み合わせ方 復習 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることがでこれらは, a n が異なるものとして区別し,お互いの位置だけを交換して得られたもので,もし a が同じものなら,これらは1つの順列となる.したがって, a を区別したときは, a が同じものであるときと比較して,それらの内部交換だけで 3!




小6 算数 小6 40 並べ方 組み合わせ方 Youtube



6年算数場合の数 1 教え方のポイント
並べ方と組み合わせ方 その1 家庭学習レシピ 並べ方と組み合わせ方 その2 家庭学習レシピ 小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちび 小学6年生の算数 場合の数 順列 練習問題プリント ちびむす ならべ方 と 組み合わせ 小学校の 場合のよって、3枚を取り出し並べるときの並べ方は、 答え 60通り 一般にn個の区別できるものの中から、r個を取り出して1列に並べることを n個のものからr個とった順列 といい、その並べ方を n P r で表します。 n P r n P r =n!/(n-r)!6年算数場合の数(1)教え方のポイント ①図や表を使って、 順序よく整理 する方法 ②図や表を使って、全部の中から 条件にあったもの の見つけ方 ③ 組み合わせや並べ方 を整理して、 落ちや重なりがない 調べ方 ④いろいろな場合を考えて、 場合を



2



1
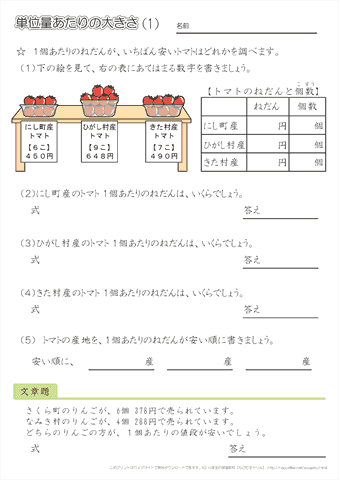
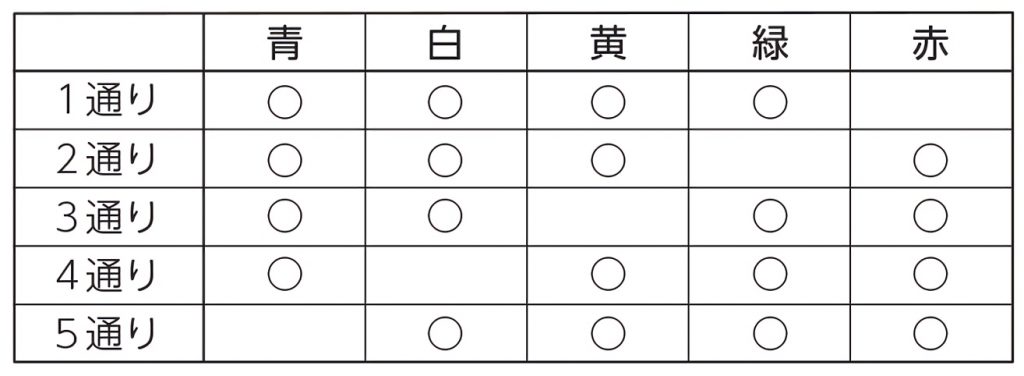
11 並べ方と組み合わせ方 学 年 組 氏 名 1 1円玉,5円玉,10円玉,100円玉,500円玉が1枚ずつあります。このうち 2枚を組み合わせてできる金額を全部いいましょう。 わせて作っていくと,10通りの金額を作ることができます。 答え 組み合わせ C とは? 組み合わせとは、 人や物を選び出す/取り出すこと です。 選び出すだけなので、選び出す順番や、選び出したものの並び順は考慮しません。 組み合わせを意味する英単語「Combination」の頭文字をとって記号「\(\mathrm{C}\)」で表します。 ボールの並べ方の組み合わせについて ボールの並べ方の組み合わせについて 手元に7つのボール、白白黒黒黄青赤のボールがあります。 このとき、白、黒が少なくとも一箇所隣り合う並べ方の組み合わせはいくつあるのかという問題があります。



6年算数場合の数 1 教え方のポイント




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
組み合わせを,図にかいて順序よく 整理して調べる。 ・探究的な活動 ・表現する活動 考 並べ方について,落ちや重なり がないように数える方法を筋道を 立てて考えている。 技 並べ方について,図を用いて落 ちや重なりがないように数えるこ とが このノートについて ももたす 小6算数でならう並べ方と組み合わせ方のところです。 並べ方 組み合わせ方 小6 算数 並べ方と組み合わせ方 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることができます! 算数「並べ方と組み合わせ方」の学習の一幕です。 5人の中から2人の掃除当番を選ぶ組み合わせ方は、全部で10通りです。 では、5人の中から3人の掃除当番を選ぶ組み合わせ方は? 図や表にかき出して、重なりを消して、、、試行錯誤しながら求めます。




すきるまドリル 小学6年生 算数 場合の数 無料学習プリント すきるまドリル 無料学習プリント




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
前のページ(組み合わせ)に戻る 教え方3 3つのものの並べ方に気づかせ、その場合の数の考え方を教えます。 問題③ くまとうさぎとしかの3匹でリレーチームをつくります。3匹の走る順番を全部かきましょう。 そして、何とおりあるか書き出しましょう。ただし,5個のボールの並び方を考える場合と違う点は, 残された三つのボールの並べ方は無視する必要がある 点です.だって,もともとは放置されていたわけですから,並び方を気にする必要はないですよね. つまり, 5個のボールの並び方の数である5!並べ方と組み合わせ方 (1) 並べ方 算数 並べ方と組み合わせ方 (2) 組み合わせ方 算数 資料の調べ方 (1) 平均とちらばり 算数 動画と連動して表示される問題に、ゲーム感覚で答えながら楽しくレッスンが
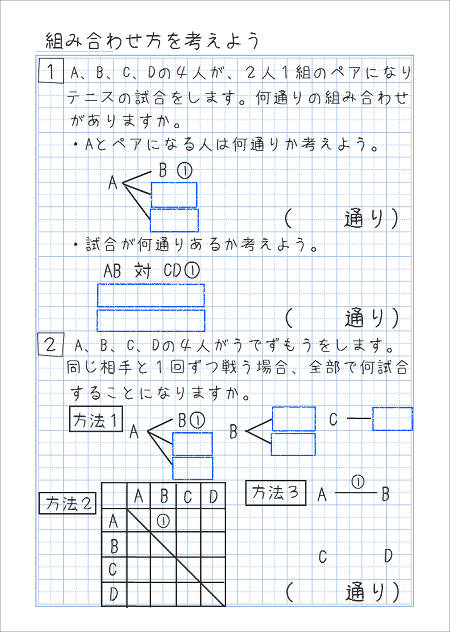



並べ方と組み合わせ方 その1 家庭学習レシピ




トップ 100 並べ方 と 組み合わせ 方 問題
次に,並べ方と組み合わせ方の違いについて順序が関係するかということに着目して比較する ことで,並べ方と組み合わせ方との意味の違いを理解することができるようにしたい。 授業Ⅰ 6年1組 36名 指導者 大山 乃輔 算数科学習指導案 小6算数『並べ方・組み合わせ』 今日は、祝日でしたが、小6算数の授業を行いました。 出席してくれた子は、「比例・反比例の復習」「並べ方・組み合わせ」の学習に励んでくれましたね。 「比例」か「反比例」か「どちらでもない」を考えるとき




小6算数 場合の数 2 指導アイデア みんなの教育技術
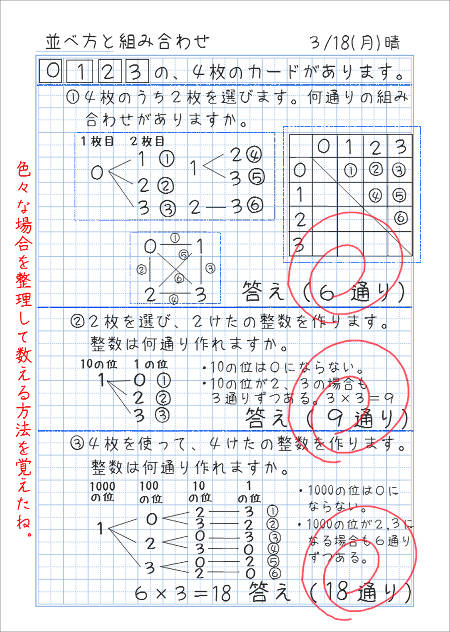



並べ方と組み合わせ方 その2 家庭学習レシピ




トップ 100 並べ方 と 組み合わせ 方 問題




掛け算 のアイデア 72 件 21 算数の教え方 学習ノート 数学 勉強



6年算数場合の数 1 教え方のポイント




荒井那奈 ほくりくアイドル部 おはきら 昨日お部屋の掃除してたら 小学校のテスト見つけたよ 高い点数いっぱい取っててびっくり やっぱり中学校のテストは難しいな 勉強がんばろーと 今日からgwおうちでのんびり過ごそうね ラッキーな




メルカリ 小学6年生 新版 くりかえし計算ドリル 学校教材 参考書 450 中古や未使用のフリマ




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典



りんご みかん バナナの3種類から重複を許して 4個取り出す組 Yahoo 知恵袋




スマホok 6年 並べ方と組み合わせ方 場合の数 並べ方を考えよう Youtube




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



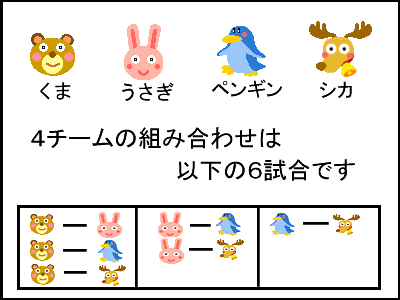
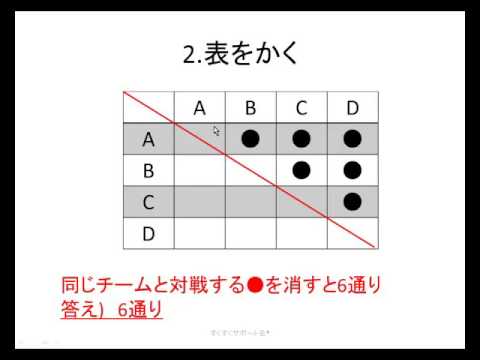
記事 詳細情報 18年 12月 11日 火曜日 6年生 算数 並べ方と組み合わせ方 a b c dの4チームでバスケットボールの試合をします どのチームも 違ったチームと1回ずつ試合をするとき どんな対戦があるか調べましょう この問題



確率の問題です A B C D Eの5人から3人の委員を選ぶとき 何 Yahoo 知恵袋




すきるまドリル 小学6年生 算数 場合の数 無料学習プリント すきるまドリル 無料学習プリント
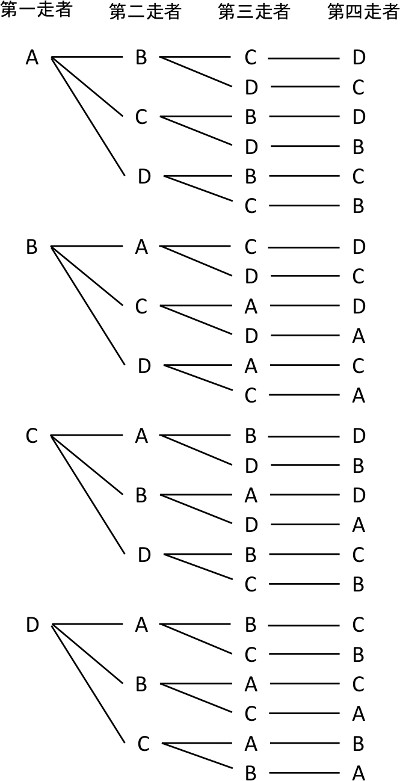



樹形図の書き方のコツと注意点 中学受験で 場合の数 をマスターする 中学受験ナビ
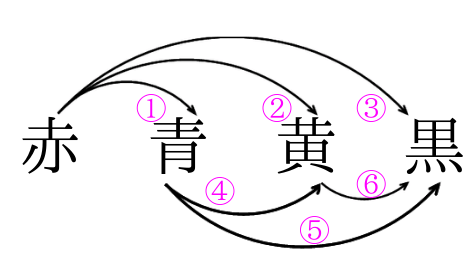



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




並べ方と組み合わせ方 算数 授業ノート 小学生 算数のノート Clear



小6算数 場合の数 2 指導アイデア みんなの教育技術




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



組み合わせ方 Youtube




数字カードの組み合わせ 家庭学習レシピ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




並べ方と組み合わせ方 その2 家庭学習レシピ




並べ方 と 組み合わせ 方 犬 イラスト



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



1




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




Catatan Tentang 算数 並べ方と組み合わせ方 Rion Clear




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




この問題の 3 の解き方が分かりません 答え見ても何言ってるのか分かりません Clear



2




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



6年算数場合の数 1 教え方のポイント
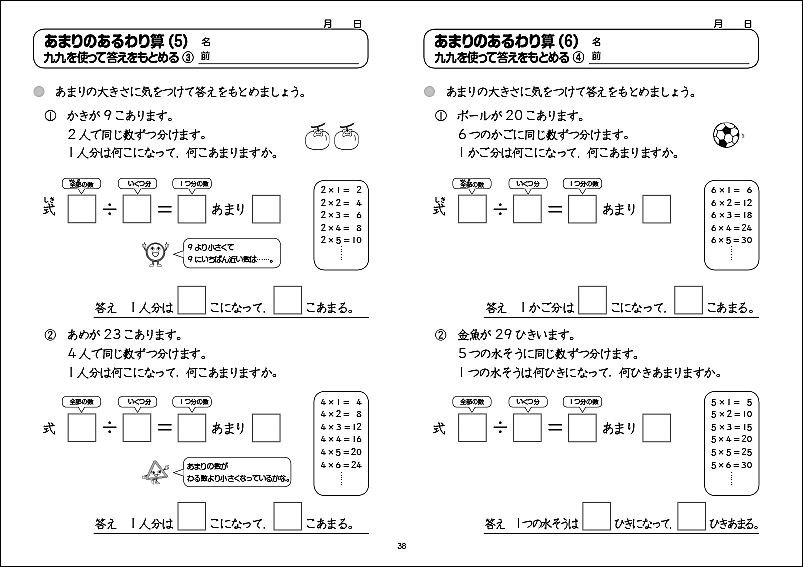



教科書算数プリント 基礎編




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




この問題を2枚目の写真の解答1の方法で解きたいのですが 答えが合いません Clear



6年算数場合の数 1 教え方のポイント
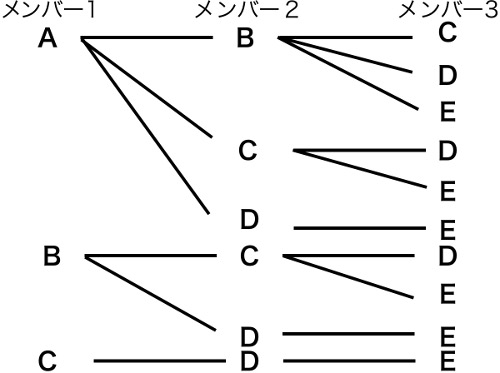



樹形図の書き方のコツと注意点 中学受験で 場合の数 をマスターする 中学受験ナビ



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




算数 場合の数の解き方は 問題別に考え方を解説 数スタ



2



1




動画で学習 1 並べ方 算数



1




4 1 Ag 7 Lihat Cara Penyelesaian Di Qanda




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生



Http Www Nagareyama Ed Jp Oyamasyou 6 1sidouann Pdf




250 300 400 450 Descubre Como Resolverlo En Qanda




無料 中2数学 発展問題 解答プリント 234 確率2 場合の数2
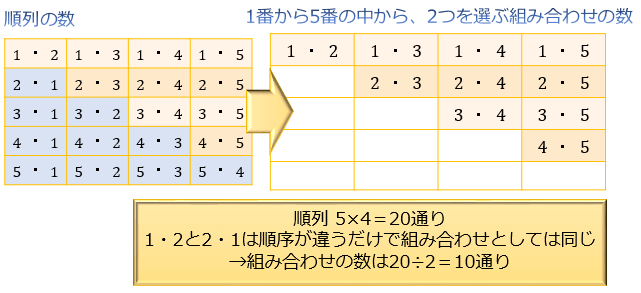



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




単元の復習にぴったり 活用力問題も あかねこ計算スキル プリントダウンロード エデュサプリ 光村教育図書
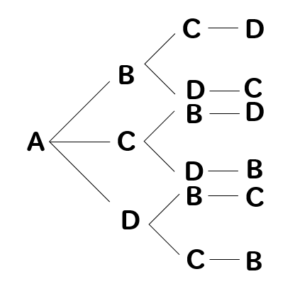



算数 場合の数の解き方は 問題別に考え方を解説 数スタ




6年算数場合の数 1 教え方のポイント
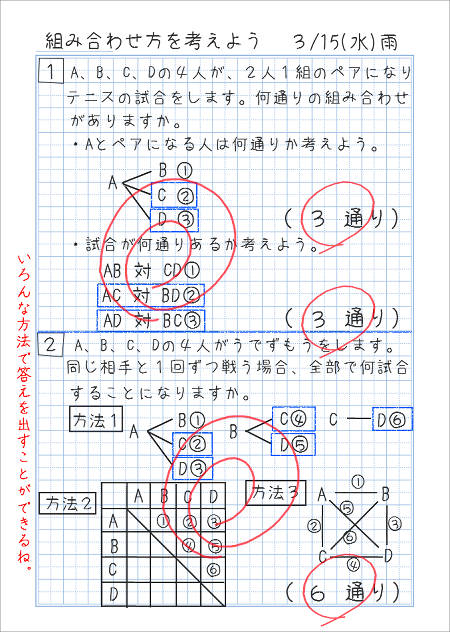



並べ方と組み合わせ方 その1 家庭学習レシピ




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




トップ 100 並べ方 と 組み合わせ 方 問題




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




志布志市立安楽小学校 学校とict sky株式会社 Ictを活用した学習活動をサポート
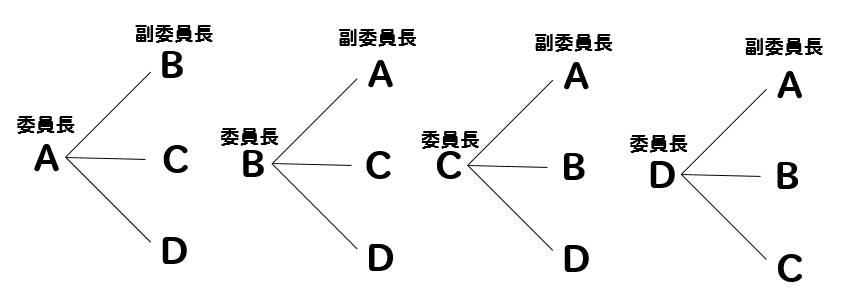



算数 場合の数の解き方は 問題別に考え方を解説 数スタ




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生



5人から3人選ぶ組み合わせは 何通りですか また 式と考え方もお願い Yahoo 知恵袋




小6 算数 小6 39 組み合わせ方 Youtube




並べ方と組み合わせ方 その1 家庭学習レシピ



トップ 100 並べ方 と 組み合わせ 方 問題




数字カードの組み合わせ 家庭学習レシピ




トップ 100 並べ方 と 組み合わせ 方 問題
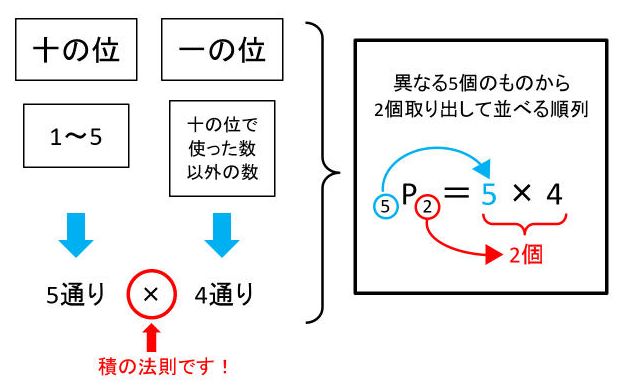



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ
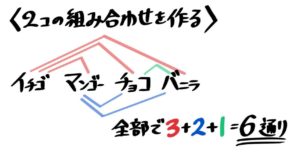



中学受験 場合の数の問題 解き方の総まとめ 数字カード 道順 色分け等 そうちゃ式 受験算数 新1号館 数論 特殊算




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ
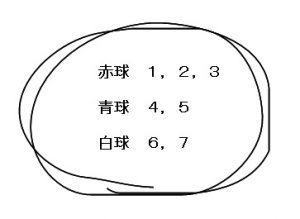



場合の数 順列と組み合わせの違いと並べ方問題の解き方




トップ 100 並べ方 と 組み合わせ 方 問題
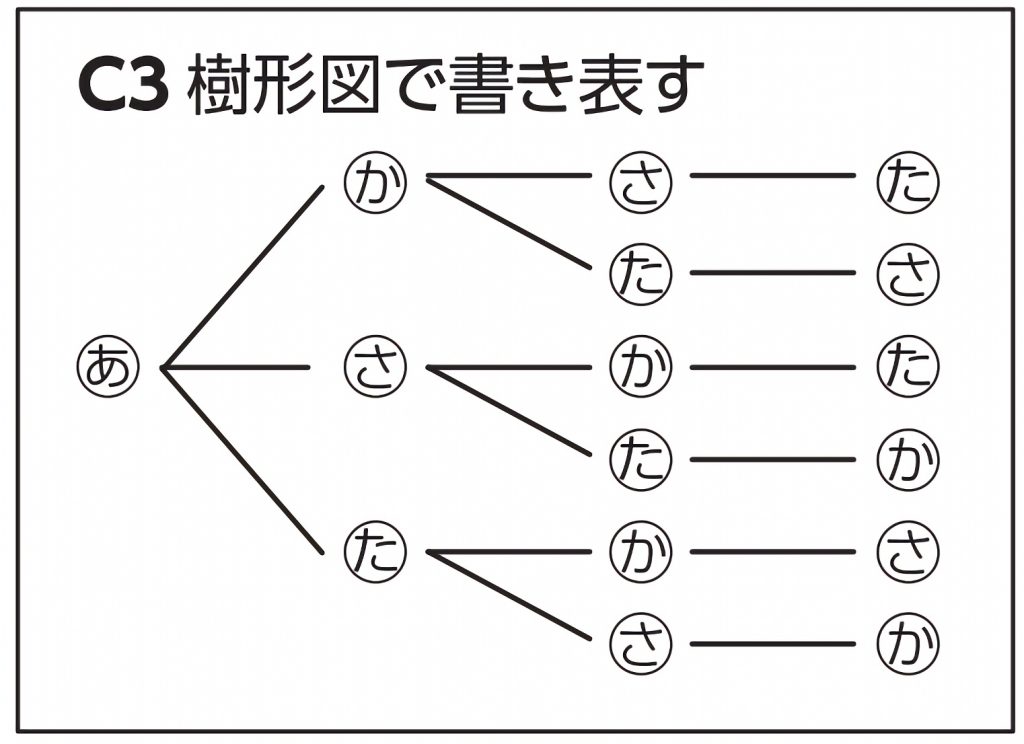



小6算数 場合の数 1 指導アイデア みんなの教育技術
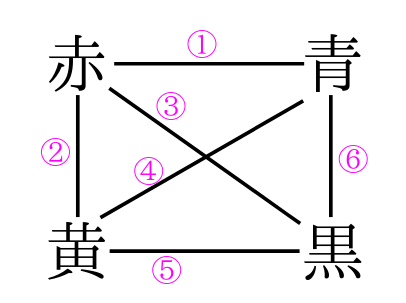



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校
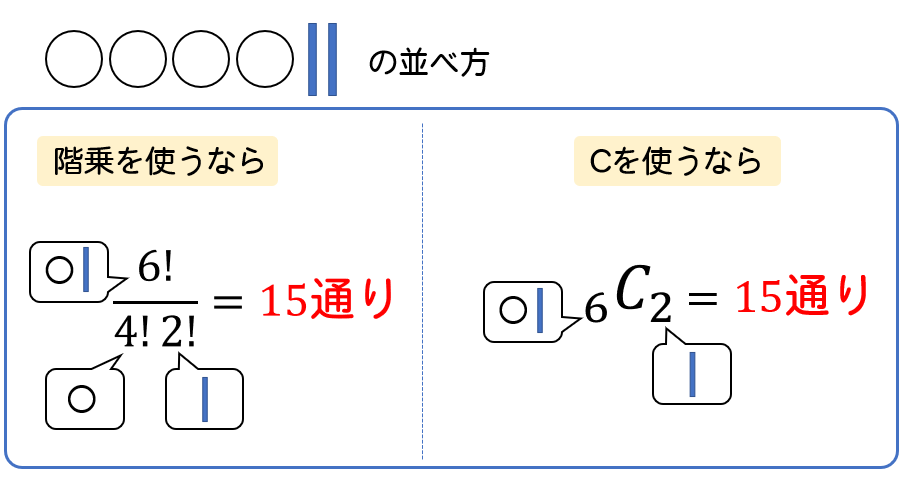



重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ
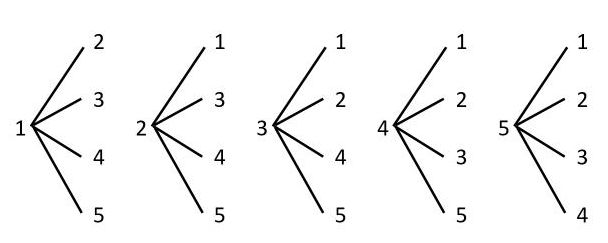



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




小学校6年 並べ方と組み合わせ方 並べ方 順列 Youtube
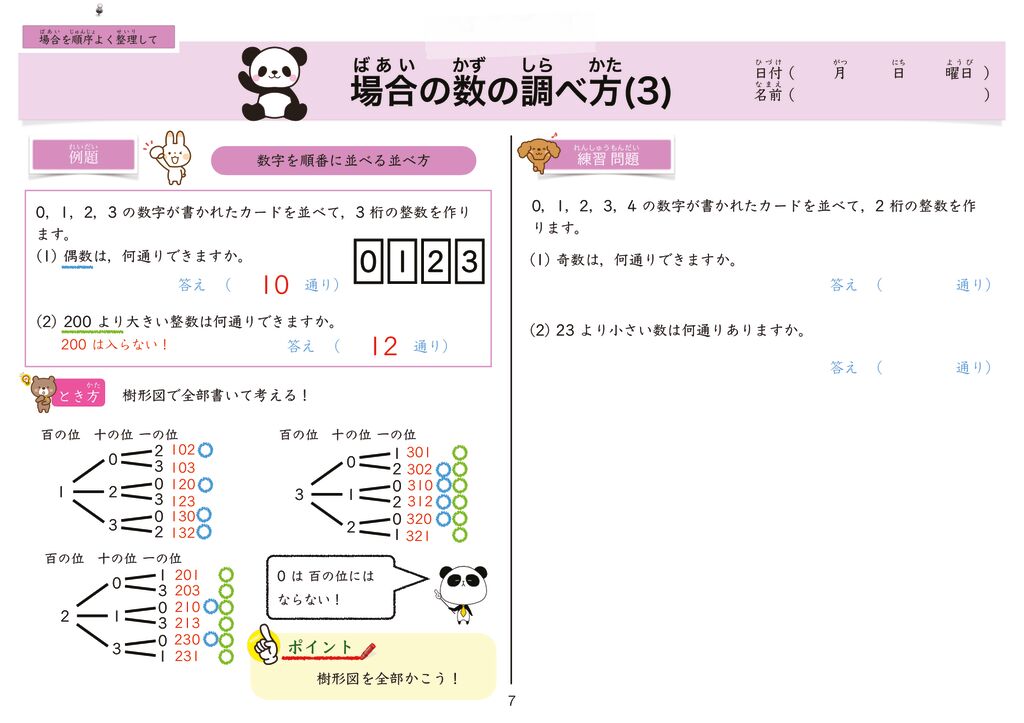



世界一分かりやすい算数 小6 場合を順序よく整理して



0 件のコメント:
コメントを投稿